categorie: Articoli in vetrina » Elettronica pratica
Numero di visite: 32001
Commenti sull'articolo: 2
Condensatori in circuiti elettronici
In articoli precedenti, abbiamo parlato brevemente del funzionamento dei condensatori nei circuiti CA, come e perché i condensatori passano la corrente CA (vedi - Condensatori CA.). In questo caso, i condensatori non si riscaldano, la potenza non viene loro assegnata: in una semionda della sinusoide, il condensatore si carica e nell'altra si scarica naturalmente, trasferendo l'energia immagazzinata alla fonte corrente.
Questo metodo di passaggio della corrente consente di chiamare il condensatore una resistenza libera ed è per questo che il condensatore collegato alla presa non fa girare il contatore. E tutto questo perché la corrente nel condensatore è in anticipo di esattamente 1/4 del tempo in cui la tensione applicata ad esso.
Ma questo avanzamento di fase consente non solo di "ingannare" il contatore, ma anche di creare vari circuiti, ad esempio generatori di segnali sinusoidali e rettangolari, ritardi temporali e vari filtri di frequenza.
Nel processo di questa storia, sarà necessario ricordare a volte ciò che è già stato detto prima, per così dire, per riassumere. Questo aiuterà a non tornare agli articoli precedenti per ricordare una semplice formula, o semplicemente "che cos'è?"
Collegamento in parallelo e in serie di condensatori
Con una connessione parallela di condensatori, la capacità totale è semplicemente la somma aritmetica delle capacità. Naturalmente, con questa inclusione, la capacità totale sarà maggiore della capacità del condensatore più grande. Totale = C1 + C2 + C3 + ... + Cn.
Nel caso di una connessione in serie, la capacità totale è inferiore a quella della più piccola.
1 / Totale = 1 / C1 + 1 / C2 + 1 / C3 + ... + 1 / Cn.
Quando due condensatori identici sono collegati in serie, la capacità totale sarà uguale alla metà della capacità di uno: ad esempio, quando si collegano due condensatori da 1 µF ciascuno, la capacità totale sarà 0,5 µF.
Capacità Xc
Qui, tutto, come quando si collegano i resistori, è esattamente l'opposto: una connessione in serie riduce la capacità totale, mentre una parallela aumenta. Questa circostanza non deve essere dimenticata quando si collegano i condensatori, poiché un aumento della capacità porta ad una diminuzione della capacità Xc
Xc = 1/2 * π * f * C.
Dal punto di vista della matematica, questo è abbastanza naturale, perché la capacità C è nel denominatore della frazione. A proposito, la frequenza f è nello stesso posto, quindi un aumento della frequenza porta anche a una diminuzione della capacità Xc. Il significato fisico di ciò è che attraverso lo stesso condensatore è meglio, più senza ostacoli, che passino le alte frequenze. Questo sarà discusso un po 'più tardi, quando si tratta dei filtri passa-basso e passa-alto.
Se prendiamo un condensatore con una capacità di 1 μF, quindi per una frequenza di 60 Hz il suo Xc sarà 2653 Ohm e per una frequenza di 400 Hz lo stesso condensatore ha un Xc di soli 398 Ohm. Chi lo desidera può controllare questi risultati con la formula, sostituendo π = 3,14, la frequenza in hertz e la capacità in farad. Quindi il risultato sarà in ohm. Tutto deve essere conforme al sistema SI!
Ma i condensatori vengono utilizzati non solo come resistenze di smorzamento a smorzamento libero o in filtri raddrizzatori. Senza la loro partecipazione, circuiti per generatori di bassa e alta frequenza, vari convertitori di forme d'onda, circuiti di differenziazione e integrazione, amplificatori e altri schemi.
Successivamente, verranno presi in considerazione vari segnali elettrici con cui devono funzionare i condensatori. Prima di tutto, si tratta di segnali periodici adatti per l'osservazione oscilloscopio.
Periodo e frequenza delle oscillazioni
L'oscillazione periodica è quindi chiamata periodica, che, senza sosta, ripete la stessa forma, ad esempio un'oscillazione sinusoidale. La durata di questa oscillazione completa è precisamente chiamata il periodo T, ed è misurata in secondi, millisecondi, microsecondi.L'elettronica moderna si occupa persino dei nanosecondi (un miliardesimo di secondo).
Il numero di periodi al secondo è chiamato frequenza (quanto spesso) delle oscillazioni f ed è espresso in hertz. 1Hz è la frequenza alla quale viene eseguita un'oscillazione, un periodo completo, in 1 secondo. Il rapporto tra periodo e frequenza è espresso dalla semplice formula T = 1 / f.
Di conseguenza, conoscendo il periodo di oscillazione, è molto semplice calcolare la frequenza f = 1 / T.
Ecco come viene calcolata la frequenza quando si misura con un oscilloscopio: viene calcolato il numero di celle in un periodo, moltiplicato per la durata di una cella e il periodo viene ottenuto, ad esempio, in microsecondi. E per scoprire la frequenza, hanno semplicemente usato l'ultima formula.
ordinario oscilloscopio elettronico Consente di osservare solo segnali periodici che possono essere sincronizzati con la frequenza di scansione per ottenere un'immagine fissa adatta alla ricerca. Se invii un segnale a un programma musicale all'ingresso dell'oscilloscopio, non sarai in grado di fermare l'immagine per nulla. Per osservare tali segnali, vengono utilizzati oscilloscopi di memorizzazione.
Quando un periodo viene misurato in millisecondi, la frequenza viene ottenuta in kilohertz, per un periodo misurato in microsecondi, la frequenza è già espressa in megahertz. Questo se non si seguono i requisiti del sistema SI: periodo in secondi, frequenza in hertz.
Vibrazioni non sinusoidali
Come accennato in precedenza, un'onda sinusoidale è la più comune e adatta allo studio e all'uso pratico della curva periodica. In condizioni industriali, è ottenuto utilizzando generatori elettrici, ad esempio nelle centrali idroelettriche. Nei dispositivi elettronici vengono utilizzate vibrazioni delle forme più diverse.
Fondamentalmente, queste sono tre forme: sinusoidale, rettangolare e triangolare, come mostrato nella Figura 1. Sia la corrente che la tensione possono avere una tale forma, quindi la figura mostra solo l'asse del tempo, l'asse delle ordinate è lasciato senza un nome.
Tali oscillazioni sono generate da speciali circuiti elettronici. I segnali rettangolari e triangolari sono spesso chiamati pulsati. Tuttavia, ci sono molti circuiti elettronici che eseguono la conversione del segnale: ad esempio un rettangolo, un triangolo può essere realizzato da una sinusoide.
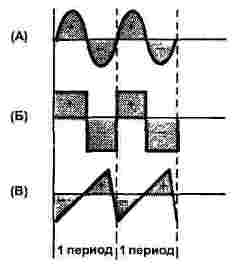
Figura 1
Per tutti e tre i segnali, la figura mostra due punti, tutti i segnali hanno la stessa frequenza.
Spettro di segnali non sinusoidali
Qualsiasi segnale elettrico può essere rappresentato come misura dell'ampiezza in un determinato momento. La frequenza di questi campioni è chiamata frequenza di campionamento e almeno due volte superiore alla frequenza superiore del segnale misurato. Quindi da questi esempi, è possibile ripristinare il segnale originale. Questo metodo viene utilizzato, ad esempio, nella registrazione audio digitale. Questo metodo è anche chiamato analisi del tempo.
Un altro metodo presuppone che qualsiasi segnale, anche rettangolare, possa essere rappresentato come la somma algebrica di sinusoidi con frequenze e fasi diverse. Questo metodo si chiama analisi di frequenza. Ma ciò che è stato detto "con frequenze diverse" non è del tutto vero: i sinusoidi costituenti sono chiamati armoniche e le loro frequenze obbediscono a determinate leggi.
Un'onda sinusoidale la cui frequenza è uguale alla frequenza di un'onda quadra è chiamata armonica fondamentale o prima. Le armoniche pari si ottengono moltiplicando la frequenza fondamentale per un numero pari e le armoniche dispari, rispettivamente, per dispari.
Pertanto, se la prima armonica ha una frequenza di 1000 Hz, la seconda è 2000 Hz, la quarta è 4000 Hz, ecc. Le armoniche dispari avranno frequenze di 3000Hz, 5000Hz. Inoltre, ogni armonica ha un'ampiezza minore di quella principale: maggiore è l'armonica, minore è l'ampiezza.
Nella musica, le armoniche sono chiamate sovratoni. Sono loro che formano il timbro del suono, rendono possibile distinguere il violino dal piano e la chitarra dal sassofono. Non consentono di confondere la voce maschile e femminile o di distinguere Petrov da Ivanov. E solo la sinusoide stessa non può più essere decomposta o assemblata da alcun segnale.
La Figura 2 mostra la costruzione di un impulso rettangolare.
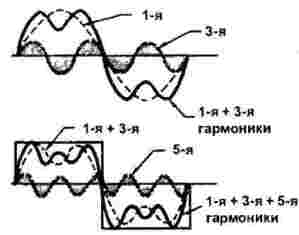
Figura 2
La prima e la terza armonica sono mostrate nella parte superiore della figura. È facile vedere che in un periodo della prima armonica tre periodi del terzo passaggio. In questo caso, l'ampiezza della terza armonica è un terzo del primo. La somma della prima e della terza armonica è anche mostrata qui.
Di seguito, insieme alla somma di 1 e 3 armoniche, vengono mostrate altre 5 armoniche: per un periodo di un segnale rettangolare riesce a fare esattamente cinque periodi. In questo caso, la sua ampiezza è ancora più piccola, più precisamente, esattamente 1/5 di quella (prima) principale. Ma non si deve pensare che tutto finisca alla quinta armonica: semplicemente non può essere mostrato nella figura, in effetti ce ne sono molti di più.
La formazione di segnali a dente di sega e triangolari, mostrata nella Figura 3, è leggermente più complicata: se nel caso precedente prendevano parte solo armoniche dispari, allora entrano in gioco anche le armoniche.
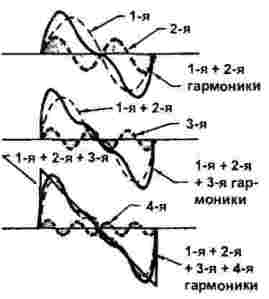
Figura 3
Pertanto, possiamo affermare che con l'aiuto di molte armoniche viene sintetizzato un segnale di qualsiasi forma e che il numero e il tipo di armoniche dipendono dalla forma d'onda, come mostrato nelle Figure 2 e 3.
Durante la riparazione e l'installazione di apparecchiature elettroniche, viene utilizzato un oscilloscopio per studiare i segnali elettrici. Ti permette di considerare la forma dei segnali periodici, la loro ampiezza, misurare il periodo di ripetizione. Ma le armoniche mostrate nelle figure 2 e 3 non sono visibili.
Anche se si collega, ad esempio, una chitarra elettrica a un oscilloscopio, si tira una corda, sullo schermo appare una sinusoide, è anche la prima armonica. In questo caso, non si può parlare di alcun tono. La stessa sinusoide risulterà se si soffia nel tubo o flauto davanti al microfono.
Come ottenere impulsi rettangolari
Dopo aver familiarizzato con i segnali elettrici, dobbiamo ricordare i condensatori con cui è iniziato l'articolo. Prima di tutto, dovresti conoscere uno dei circuiti elettronici classici - multivibratore, (Figura 4) è lui che genera impulsi rettangolari. Il circuito è così classico che inizia a funzionare immediatamente senza richiedere impostazioni o regolazioni.
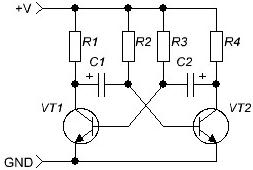
Figura 4
Il multivibratore è un amplificatore a due stadi, coperto da feedback positivo. Se i resistori di carico del collettore R1 = R4, i resistori di base R2 = R3 sono uguali e i condensatori C1 = C2 sono uguali, il multivibratore è chiamato simmetrico e genera impulsi ad onda quadra del tipo meandro - la durata dell'impulso è uguale alla durata della pausa.
Il ciclo di lavoro di tali impulsi (il rapporto tra il periodo e la durata dell'impulso) è uguale a due. Negli schemi in lingua inglese, tutto è esattamente l'opposto: lo chiamano duty cycle. Viene calcolato come rapporto tra la durata dell'impulso e il periodo della sua successione ed è espresso in percentuale. Pertanto, per il meandro, il ciclo di lavoro è del 50%.
Il computer è corretto?
Il nome multivibratore è stato proposto dal fisico olandese van der Pol, perché lo spettro di un segnale rettangolare contiene molte armoniche. È possibile verificarlo se è possibile posizionare un ricevitore radio che opera nella gamma delle onde medie vicino a un multivibratore che funziona anche a una frequenza audio: ululati provengono dall'altoparlante. Ciò suggerisce che oltre alla frequenza del suono, il multivibratore emette anche oscillazioni ad alta frequenza.
Per determinare la frequenza di generazione, si può usare la formula f = 700 / (C1 * R2).
Con questa forma della formula, la capacità del condensatore in microfarad (μF), la resistenza in chilo-ohm (KΩ), il risultato in hertz (Hz). Pertanto, la frequenza è determinata dalla costante di tempo del circuito C1 * R2; i carichi del collettore non influiscono sulla frequenza. Se prendiamo C1 = 0,02 μF, R2 = 39 KΩ, otteniamo f = 700 / (0,02 * 39) = 897,4 Hz.
Multivibratore nell'era dei computer e microcontrollori Secondo questo schema, non viene quasi mai utilizzato, sebbene possa essere adatto a vari esperimenti. Prima di tutto, usando i computer. Ecco come appare il circuito multivibratore assemblato nel programma Multisim. Qui è anche mostrato il collegamento dell'oscilloscopio.
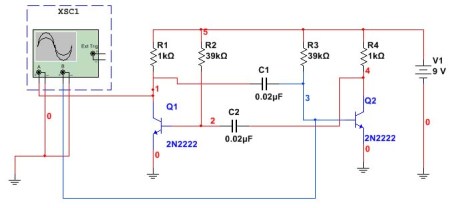
Figura 5
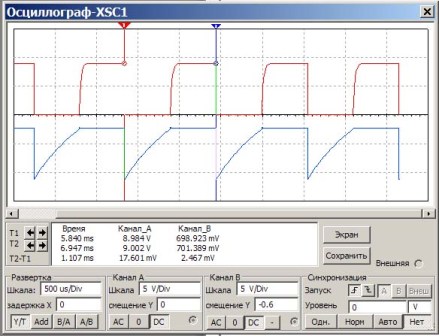
In questo circuito, condensatori e resistori sono installati come nell'esempio precedente. Il compito è controllare il calcolo in base alla formula se si otterrà la stessa frequenza. Per fare ciò, misurare il periodo degli impulsi, quindi ricalcolarli in frequenza. Il risultato dell'oscilloscopio Multisim è mostrato nella Figura 6.
Figura 6
Alcuni chiarimenti alla Figura 6.
Sullo schermo dell'oscilloscopio, l'impulso rosso mostra gli impulsi sul collettore a transistor e il blu sulle basi. Sotto lo schermo in una grande finestra bianca, i numeri mostrano i risultati della misurazione. Siamo interessati alla colonna "Tempo". Il tempo è misurato dagli indicatori T1 e T2 (triangoli rossi e blu sopra lo schermo).
Pertanto, il periodo di ripetizione dell'impulso T2-T1 = 1.107ms viene mostrato in modo abbastanza accurato. Resta solo da calcolare la frequenza f = 1 / T = 1 / 1.107 * 1000 = 903Hz.
Il risultato è quasi lo stesso del calcolo secondo la formula, che viene data un po 'più alta.
I condensatori possono essere utilizzati non solo separatamente: in combinazione con resistori, consentono di creare semplicemente vari filtri o creare circuiti di sfasamento. Ma questo sarà discusso nel prossimo articolo.
Continuazione dell'articolo: Condensatori in circuiti elettronici. Parte 2
Boris Aladyshkin
Vedi anche su electro-it.tomathouse.com
: