"Tutto scorre", o legge di Ohm per i curiosi

Anche l'ultimo mocassino, dopo aver studiato per qualche tempo in prima media, lo dirà all'insegnante Legge di Ohm - questo è "U è uguale a I volte R". Sfortunatamente, lo studente eccellente più intelligente dirà poco di più: il lato fisico della legge di Ohm rimarrà un mistero per lui per sette sigilli. Mi permetto di condividere con i miei colleghi la mia esperienza nel presentare questo argomento apparentemente primitivo.

L'oggetto della mia attività pedagogica era l'arte e la terza media umanitaria, i cui interessi principali, come intuisce il lettore, erano molto lontani dalla fisica. Ecco perché l'insegnamento di questa materia è stato affidato all'autore di queste righe, che, in generale, insegna biologia. E 'stato qualche anno fa.

La lezione sulla legge di Ohm inizia con la banale affermazione che la corrente elettrica è il movimento di particelle cariche in un campo elettrico. Se solo una forza elettrica agisce su una particella carica, allora la particella accelera secondo la seconda legge di Newton. E se il vettore della forza elettrica che agisce sulla particella carica è costante sull'intera traiettoria, allora è ugualmente accelerato. Proprio come un peso cade sotto l'influenza della gravità.

Ma qui il paracadutista cade completamente sbagliato. Se trascuriamo il vento, il suo tasso di caduta è costante. Anche uno studente nell'arte e nella classe umanitaria risponderà che oltre alla forza di gravità, un'ulteriore forza agisce sul paracadute che cade - la forza della resistenza aerea. Questa forza è uguale in valore assoluto alla forza di attrazione del paracadute da parte della Terra ed è opposta ad essa nella direzione. Perché? Questa è la domanda chiave della lezione. Dopo alcune discussioni, concludiamo che la forza di resistenza aumenta con l'aumentare del tasso di caduta. Pertanto, il corpo che cade accelera a una velocità alla quale la gravità e la resistenza dell'aria si equivalgono e il corpo cade ulteriormente a una velocità costante.

È vero, nel caso di un paracadutista, la situazione è un po 'più complicata. Il paracadute non si apre immediatamente e il paracadutista accelera a una velocità significativamente più elevata. E quando il paracadute si è già aperto, la caduta inizia con una decelerazione, che continua fino a quando la forza di gravità e la forza della resistenza dell'aria non vengono bilanciate.

Per un carico di paracadute con una massa totale m che scende a velocità costante v, possiamo scrivere: mg - F (v) = 0, dove F (v) È la forza di resistenza dell'aria, considerata in funzione del tasso di caduta. Per quanto riguarda la forma della funzione F (v) possiamo dire solo una cosa finora: sta crescendo monotonamente. Questa circostanza fornisce la stabilizzazione della velocità.

Nel caso più semplice, quando F (v) = k, la velocità costante con cui cadrà il paracadute sarà pari a mg / k. Facciamo qualche conversione ora. Lascia cadere il paracadute da un'altezza h. Quindi la differenza nelle energie potenziali del corpo prima e dopo la caduta sarà uguale a mgh = mU, dove U è l'energia potenziale di un corpo di massa unitaria ad un'altezza h, o la differenza potenziale del campo gravitazionale nei punti iniziale e finale di incidenza.

Alla luce di quanto precede, otteniamo la formula: F (v) = mU / h. (1)

E ora torniamo al conduttore attraverso il quale scorre la corrente elettrica. Un gran numero di particelle cariche si muove lungo il conduttore, che si scontrano con gli atomi più spesso più velocemente volano. L'analogia con la discesa di un paracadute è abbastanza trasparente, l'unica differenza è che ci sono molti "paracadute" e non si muovono nel campo gravitazionale, ma nel campo elettrico. Date queste circostanze, (1) può essere riscritto nella forma: F (v) = eU / l, (2)

dove e è la carica di particelle, U è la differenza di potenziale elettrico alle estremità del conduttore, l è la lunghezza del conduttore.La forza attuale è ovviamente uguale a I = neS, dove n è il numero di particelle cariche per unità di volume, S è l'area della sezione trasversale del conduttore, è la velocità delle particelle (per semplicità, supponiamo che tutte le particelle cariche siano uguali).

Per ottenere la dipendenza I (U), è necessario conoscere esplicitamente la dipendenza F (). L'opzione più semplice (F = k) dà immediatamente la legge di Ohm (I ~ U):

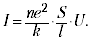
Il valore si chiama conducibilità e il reciproco di esso si chiama resistenza. In onore dello scopritore della legge, la resistenza è di solito espressa in ohm.

Il valore (ne2 / k) è chiamato conducibilità specifica e il suo valore inverso è chiamato resistenza specifica. Questi valori caratterizzano il materiale di cui è composto il conduttore. È significativo che la conduttività sia proporzionale al numero di particelle cariche per unità di volume (n). Nelle soluzioni di metalli ed elettroliti, questo numero è grande, ma nei dielettrici è piccolo. Il numero di particelle cariche per unità di volume di un gas può dipendere dal campo applicato (cioè è una funzione di U); pertanto, la legge di Ohm non si applica ai gas.

Nel derivare la legge di Ohm, abbiamo fatto un'ipotesi non ovvia. Abbiamo accettato che la forza che inibisce il movimento di una particella carica è proporzionale alla sua velocità. Certo, si potrebbe provare a giustificare questa idea in qualche modo, ma la verifica sperimentale sembra molto più convincente.

Una verifica sperimentale di questa ipotesi è, ovviamente, una verifica della stessa legge di Ohm, cioè proporzionalità di U e I. Sembrerebbe che questo non sia difficile: abbiamo un voltmetro e un amperometro! Ahimè, non tutto è così semplice. Dobbiamo spiegare ai nostri studenti che un voltmetro, proprio come un amperometro, non misura la tensione, ma la forza attuale. E abbiamo il diritto di impostare volt sulla scala del voltmetro solo perché inizialmente conosciamo la legge di Ohm, che vogliamo verificare. Hai bisogno di altri approcci.

Ad esempio, puoi usare la seguente idea. Colleghiamo n batterie in serie e supponiamo che in questo caso la tensione sia aumentata n volte. Se la legge di Ohm è vera, allora anche la forza attuale aumenterà n volte, per cui il rapporto n / I (n) non dipenderà da n. Questa ipotesi è giustificata dall'esperienza. È vero, le batterie hanno anche una resistenza interna, motivo per cui il valore di n / I (n) cresce lentamente all'aumentare di n, ma non è difficile correggerlo. (Lo stesso G. Ohm ha misurato lo stress in modo diverso, di cui gli studenti possono leggere nel libro di testo di G.Ya. Myakishev e altri.)

Facciamo la domanda: "" Nella lontana costellazione di Tau Ceti ", non la legge di Ohm, ma la legge del grande scienziato locale Academic X. Secondo la legge di X, la forza attuale è proporzionale al quadrato della differenza potenziale alle estremità del conduttore. In che modo la forza frenante delle particelle dipende dalla loro velocità sul Tau Ceti? ” Con l'aiuto di semplici trasformazioni, gli studenti giungono alla conclusione che la forza è proporzionale alla radice quadrata della velocità.

E ora passiamo a un altro processo: il movimento dell'acqua in un tubo, al termine del quale vengono create diverse pressioni. Qui abbiamo una situazione completamente diversa: non le singole particelle in movimento si sfregano contro un materiale stazionario distribuito sull'intero volume del conduttore, ma gli strati di particelle in movimento si sfregano l'una contro l'altra. E questa circostanza cambia radicalmente tutto il ragionamento fisico.

Due forze agiscono su uno strato separato di acqua che si muove in un tubo:

a) la differenza nelle forze di pressione alle estremità dello strato;

b) la forza di attrito contro i vicini strati di acqua.

Se viene stabilita una velocità costante dello strato, queste forze sono uguali e dirette in direzioni opposte.

La forza di attrito contro gli strati d'acqua vicini può rallentare il movimento se e solo se diversi strati d'acqua si muovono a velocità diverse. In un conduttore, la velocità delle particelle cariche non dipende dal fatto che si trovino sul bordo del conduttore o al suo centro, ma l'acqua al centro del tubo si muove rapidamente e lentamente lungo i bordi, sulla stessa superficie del tubo, la velocità dell'acqua è zero.

Un analogo dell'intensità attuale può essere considerato flusso d'acqua, ad es. la quantità di acqua che esce dal tubo per unità di tempo. Poiché la velocità dell'acqua nei diversi strati non è la stessa, calcolare la portata non è così semplice.Un analogo della differenza nei potenziali elettrici è la differenza di pressione alle estremità del tubo.

Proprio come in un conduttore con corrente, si osserva una proporzionalità diretta nel tubo con acqua tra la differenza di pressione alle estremità e la portata. Ma il coefficiente di proporzionalità è completamente diverso. Innanzitutto, la portata dell'acqua dipende non solo dall'area della sezione trasversale del tubo, ma anche dalla sua forma. Se il tubo è cilindrico, la portata è direttamente proporzionale non all'area della sezione trasversale, ma al suo quadrato (cioè il raggio al quarto grado). Questa dipendenza si chiama legge Poiseuille.

Ecco il momento di ricordare il corso di anatomia, fisiologia e igiene, studiato in prima media. Il corpo umano ha un gran numero di vasi collegati in parallelo. Supponiamo che una di queste navi si sia espansa e che il suo raggio sia leggermente, solo raddoppiato, aumentato. Quante volte, con la stessa pressione alle estremità della nave, aumenterà la quantità di sangue che la attraversa? L'area della sezione trasversale è proporzionale al quadrato del raggio e il quadrato dell'area della sezione trasversale è proporzionale al raggio del quarto grado. Pertanto, quando il raggio viene raddoppiato, il flusso sanguigno aumenta di 16 (!) Volte. Tale è il potere della legge di Poiseuille, che consente di creare un meccanismo molto efficace per ridistribuire il sangue tra gli organi. Se gli elettroni non fluissero attraverso i vasi sanguigni, il loro flusso aumenterebbe solo quattro volte.

La descrizione dell'argomento sopra descritto è diversa da quella tradizionale. In primo luogo, vengono dedicate tre lezioni all'argomento che, con l'attuale carenza di ore, può essere considerato un lusso inammissibile per le scienze naturali. Tuttavia, ciò è giustificato dal fatto che è possibile rivelare in modo abbastanza semplice e popolare il significato fisico della legge e dotare gli studenti di una metodologia che possono utilizzare per analizzare una varietà di processi fisici: la caduta di un corpo in aria, il movimento di un fluido in un tubo, il movimento di particelle cariche lungo un conduttore e in seguito nell'analisi del passaggio della corrente elettrica attraverso il vuoto e i gas.

Questo approccio si chiama integrazione intradisciplinare. Con il suo aiuto, abbiamo dimostrato agli studenti le caratteristiche comuni a distanza, a prima vista, sezioni della fisica, abbiamo dimostrato che la fisica non è un "gruppo" di "leggi fisiche" che non sono collegate tra loro, ma un edificio snello. Lo stesso vale, ovviamente, per altre discipline scientifiche. E così, sembrerebbe, uno spreco irrazionale di ore di formazione sta dando i suoi frutti.

Leggi anche:Come usare un multimetro