Algebra booleana. Parte 1. Un po 'di storia

A scuola studiavamo tutti l'algebra, ma lì non parlavano di algebra booleana. Qual è la differenza tra l'algebra booleana e l'algebra scolastica, la storia del suo aspetto, i problemi e le applicazioni sono descritte in questo articolo.

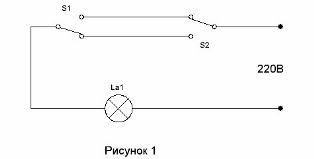
Il circuito che consente a due interruttori di accendere la luce nel corridoio all'ingresso del corridoio e spegnerlo quando si entra nella stanza è noto da molto tempo (vedi. Circuito di controllo dell'illuminazione del corridoio). È mostrato in Figura 1.

Compito numero 1. Più complicato Crea un diagramma che ti consente di accendere e spegnere la luce nella tua stanza con uno dei 3 diversi interruttori. Gli interruttori si trovano all'ingresso della stanza, sopra il letto e alla scrivania.

Compito numero 2.

In un comitato sportivo, come un comitato di fabbrica, si sono riuniti 5 giudici.

Ognuno di loro deve votare per decisioni diverse. La decisione è adottata a maggioranza dei voti, ma solo a condizione che il presidente della commissione voti a favore.

I giudici votano premendo il pulsante che chiude l'interruttore situato sotto il tavolo in cui sono seduti. Chiudendo l'interruttore, votano a favore, disconnettendo i contro. Disegna un semplice diagramma che ti consente di vedere automaticamente i risultati della votazione. Nel caso più semplice, semplicemente con l'aiuto di una lampadina - illuminata - la decisione viene presa, non si accende - no.

Compito numero 3. In pratica, questo è improbabile, ma poiché un compito educativo complesso è abbastanza adatto.

In una grande stanza esagonale, un interruttore è installato su ogni parete. Costruisci un circuito in modo da poter accendere o spegnere la luce nella stanza in qualsiasi momento ruotando un (qualsiasi) interruttore.

Dopo esserti seduto per tre o quattro giorni senza successo, mettili da parte temporaneamente. E occupati Algebra booleana. È algebra booleana o, come viene anche chiamata, Algebra booleana, algebra del circuito relè, ti aiuterà a risolvere i tuoi problemi.

Cos'è l'algebra booleana?

Stranamente, nonostante il fatto che per cinque anni abbiano studiato l'algebra a scuola, molti studenti, e in seguito adulti, non saranno in grado di rispondere alla domanda, cos'è l'algebra? L'algebra è una scienza che studia gli insiemi di alcuni elementi e le azioni su di essi.

In un corso di algebra, tali elementi sono numeri. I numeri possono essere indicati non con i numeri, ma con le lettere, tutti lo conoscono. Nelle prime lezioni di algebra, questo rende sempre difficile per molti studenti. Ricorda quanto all'inizio fosse difficile abituarsi a piegare lettere anziché numeri, risolvendo equazioni che non dicevano nulla.

Probabilmente ognuno di noi si è posto la domanda: "Perché dobbiamo inserire lettere anziché numeri ed è necessario?" E solo più tardi hai visto quali vantaggi offre l'algebra nella risoluzione dei problemi rispetto all'aritmetica.

L'algebra è usata in molte scienze esatte. Questa è fisica, meccanica, sopromat, elettricità. Legge di Ohm non c'è nient'altro che un'equazione algebrica: è sufficiente sostituire i loro valori numerici anziché le lettere per scoprire quale corrente scorrerà nel carico o quale resistenza ha una sezione del circuito.

Così hai conosciuto l'algebra dei numeri o l'algebra elementare. Il compito principale e quasi unico è ottenere una risposta alla domanda: “A cosa equivale X? Quanto?

Al liceo, studiano gli inizi dell'algebra vettoriale. Questa algebra è fondamentalmente diversa dall'algebra elementare. Ha una diversa natura dell'insieme studiato e altre regole di azione. Risolvendo l'equazione dei vettori, otteniamo nella risposta un vettore che non è un numero ordinario che risponde alla domanda "Quanto?"

Le formule dell'algebra vettoriale sono per molti aspetti diverse dalle formule dell'algebra elementare. Ad esempio, nell'algebra elementare e nell'algebra vettoriale vi è un'operazione di aggiunta. Ma viene eseguito in modi completamente diversi.L'aggiunta di numeri non è affatto uguale all'aggiunta di vettori.

Esistono altre algebre: algebra lineare, algebra delle strutture, algebra degli anelli, algebra della logica o, al contrario, algebra booleana. Probabilmente non hai sentito il nome nelle lezioni di scuola. George Boole - ma tutti conoscono il nome di una delle sue talentuose figlie Ethel Voinich (1864-1960). Ha scritto il romanzo "Gadfly", che parla della lotta per i diritti dei carbonaristi italiani.

George Bull nacque in Inghilterra il 2 novembre 1815. Per tutta la vita ha lavorato come insegnante di matematica e fisica a scuola. Dalle memorie dei suoi studenti è noto quale grande importanza attribuiva Bul allo sviluppo delle capacità creative degli studenti. Nell'introdurre nuovo materiale, ha cercato di garantire che i suoi stessi studenti "riscoprissero" determinate formule e leggi.

Raccontando agli studenti le difficoltà che inevitabilmente gli scienziati hanno dovuto affrontare nella ricerca della verità, all'insegnante piaceva ripetere una saggezza orientale: anche il trono persiano non può portare tanto piacere a una persona quanto la più piccola scoperta scientifica. Buhl non perse mai la speranza che un giorno i suoi studenti avrebbero fatto una vera scoperta.

La gamma di interessi scientifici di Buhl era molto ampia: era altrettanto interessato alla matematica e alla logica - la scienza delle leggi e delle forme di pensiero. A quei tempi, la logica era considerata una scienza umanitaria e molti di coloro che conoscevano George Boole erano stupiti di come i metodi esatti di cognizione inerenti alla matematica e i metodi di logica puramente descrittivi potessero coesistere in una persona.

Ma lo scienziato voleva rendere la scienza delle leggi e delle forme di pensiero rigorosa come una qualsiasi delle scienze naturali, per esempio matematica e fisica. Per fare questo, Boule iniziò a indicare non numeri come lettere, come avviene nella normale algebra, ma affermazioni e dimostrò che tali equazioni, molto simili a quelle algebriche, possono risolvere domande sulla verità e sulla falsità delle dichiarazioni fatte dall'uomo. Così nacque l'algebra booleana.

Ma molto prima di George Boole, il matematico e filosofo tedesco Gottfried Leibniz (1646–1716) espresse per la prima volta l'idea di creare una scienza che designasse tutti i concetti del discorso colloquiale ordinario con simboli e stabilisse una nuova algebra per combinare questi simboli.

Dopo la creazione di una tale scienza, secondo Leibniz, scienziati e filosofi smetteranno di litigare e urlare a vicenda, scoprire la verità, ma prenderanno una matita e diranno con calma: "Calcoliamo!"

Oggi l'algebra della logica è diventata una parte importante della matematica. Uno dei suoi compiti è la soluzione di tutti i tipi di equazioni, i cui rapporti numerici sono sostituiti da quelli alfabetici. Ognuno di voi, probabilmente, per tutta la vita ha ricordato come risolvere le equazioni di secondo e terzo grado con coefficienti di lettere. Quindi, Boole nella sua nuova algebra ha usato tutte queste formule e regole.

La novità dell'algebra booleana è che gli elementi dell'insieme in cui sono studiati non sono numeri, ma affermazioni. Se, quando si risolvono le equazioni algebriche ordinarie, viene determinato quale numero è uguale a X sconosciuto, l'algebra della scuola cerca la risposta alla domanda: "Quanto?"

L'algebra della logica sta cercando la risposta alla domanda: "Questa o quella affermazione indicata con la lettera X è vera?"

Il significato e il contenuto della dichiarazione non svolgono alcun ruolo qui. Ogni affermazione può essere solo vera o falsa. Non può essere metà vero e metà falso. Ad esempio, possiamo ricordare di aver lanciato un sacco con una moneta.

Qui vengono considerati solo due stati di moneta: testa o croce. Previo accordo delle parti, l'aquila è SÌ e le code sono NO. Nessun altro punto intermedio viene preso in considerazione nella teoria della probabilità, sebbene sia possibile. Una moneta lanciata può cadere su un bordo, rotolare giù dal pavimento fino alle gambe di una sedia o di un tavolo e rimanere in posizione verticale, o persino cadere in un ampio spazio nel pavimento. (Per analogia con i circuiti elettrici, le ultime due situazioni possono essere considerate un malfunzionamento sotto forma di un contatto bruciato).Ma a quei tempi l'algebra booleana, purtroppo, non era ampiamente usata.

Claude Shannon "scoprì" di nuovo l'algebra di Buhl. Nel 1938, mentre era ancora uno studente presso il Massachusetts Institute of Technology e l'America, il giovane Claude dimostrò che l'algebra booleana è completamente adatta per l'analisi e la sintesi di relè e circuiti di commutazione.

Con l'aiuto dell'algebra booleana, è molto facile realizzare un circuito elettrico di un automa che opera su un relè.Per questo, si scopre, devi solo sapere esattamente cosa dovrebbe fare la macchina, cioè devi avere un algoritmo per il suo funzionamento. Quindi sono state gettate le basi per la teoria delle macchine digitali che operano secondo il principio SÌ o NO.

Tale, in breve, è la storia dell'algebra booleana. Nei seguenti articoli considereremo le sue leggi di base, esempi di circuiti di contatto che attuano tali leggi. Considera la soluzione di quei compiti che sono stati assegnati all'inizio dell'articolo.

Continuazione dell'articolo: Algebra booleana. Parte 2. Leggi e funzioni di base

Boris Aladyshkin