categorie: Articoli in vetrina » Elettricisti alle prime armi
Numero di visite: 57937
Commenti sull'articolo: 4
Algebra booleana. Parte 3. Schemi di contatto
 L'articolo descrive i principi di base della progettazione di circuiti a relè secondo un determinato algoritmo del loro funzionamento.
L'articolo descrive i principi di base della progettazione di circuiti a relè secondo un determinato algoritmo del loro funzionamento.
In due articoli precedenti è stato detto sulle basi Algebra booleana e algebra di relè. Su questa base, sono state sviluppate formule strutturali e su di esse sono stati sviluppati circuiti di contatto già tipici.
Redigere una formula strutturale secondo uno schema già pronto è una questione semplice. È molto più difficile presentare il circuito elettrico della futura macchina secondo la formula strutturale già pronta. Ha bisogno di un po 'di allenamento!
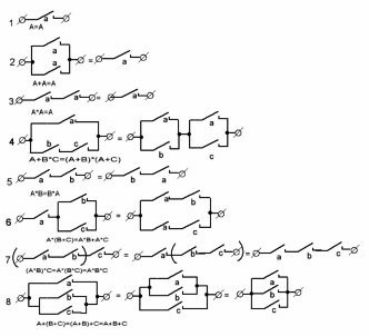
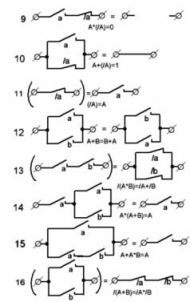
La Figura 1 mostra le opzioni più comuni. circuiti di contatto e loro equivalenti. Aiuteranno nella preparazione dei circuiti elettrici delle macchine e analizzeranno le strutture già pronte, ad esempio durante il processo di riparazione.
Come è possibile utilizzare le opzioni per i circuiti di contatto discussi sopra?
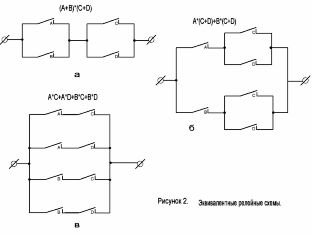
Considera il circuito mostrato in Figura 2, a. La formula strutturale corrispondente ha la forma: (A + B) * (C + D).
Usando la legge di distribuzione dell'algebra booleana, apriamo le parentesi in questa espressione e otteniamo: A * (C + D) + B * (C + D), che corrisponde allo schema mostrato nella Figura 2, b. Inoltre, a causa della moltiplicazione, possiamo ottenere la formula A * C + A * D + B * C + B * D, corrispondente alla Figura 2, c.
Tutti e tre gli schemi sono equivalenti, ovvero risultano chiusi alle stesse condizioni. Tuttavia, sono diversi per complessità.
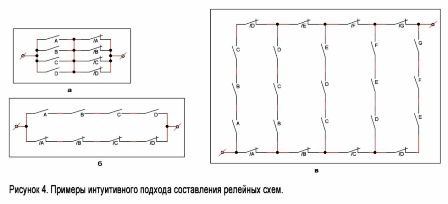
Figura 1. Circuiti di contatto tipici
Il primo dei circuiti, il più semplice, richiede quattro relè, ognuno dei quali deve avere un contatto normalmente aperto. (Per semplificare i disegni, le bobine dei relè non sono mostrate).
Lo schema "b" richiede un relè con due gruppi di contatti. In realtà, il compito principale dell'algebra dei circuiti di contatto è quello di trovare tutti i circuiti equivalenti in modo da poter scegliere quello più semplice da essi.
Figura 2. Circuiti di contatto equivalenti.
Per consolidare il materiale coperto, provare a risolvere personalmente i seguenti problemi.
1. Disegnare lo schema circuitale di un automa con la formula strutturale A * B * C * D + A * B * E + A * D.
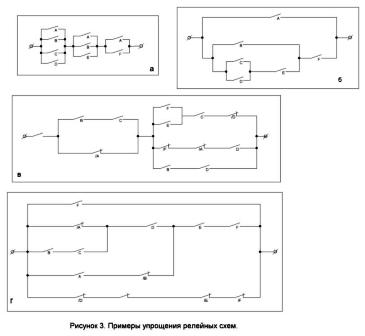
2. Dimostrare che i circuiti mostrati nella Figura 3, aeb, sono equivalenti.
3. Semplificare il circuito mostrato in Figura 3, c.
4. Quale formula strutturale implementa lo schema di Figura 3, d?
Dopo quello che abbiamo già studiato, sarà possibile iniziare a risolvere i problemi che erano stati posti all'inizio del primo articolo. Li ricordiamo brevemente.
Il primo compito era accendere e spegnere la lampadina nella stanza con tre interruttori situati in luoghi diversi: alla porta, al tavolo, al letto.
Il secondo compito è quello di votare i giudici sportivi: su quattro giudici "FOR" deve votare almeno due, a condizione che "FOR" abbia votato il presidente della commissione.
Il terzo compito era solo a scopo educativo. Propose lo stesso del primo, solo per sei interruttori, come se ci fossero sei pareti nella stanza. Circuiti simili sono appena stati sviluppati utilizzando l'algebra dei circuiti di relè.
In generale, se vogliamo sviluppare uno schema che abbia determinate proprietà logiche, allora possiamo affrontare questo problema in due modi diversi. Convenzionalmente, questi percorsi possono essere definiti "intuitivi" e "algebrici".
Alcuni compiti sono meglio risolti nel primo modo, mentre altri nel secondo. L'approccio intuitivo risulta essere più conveniente quando il funzionamento del circuito è controllato da molti interruttori, ma vi è una certa simmetria nella disposizione reciproca di questi relè. Vedremo che qui un approccio intuitivo porta più velocemente all'obiettivo, mentre l'uso dell'apparato di algebra di relè nel caso di molte variabili può essere molto complicato. È utile conoscere entrambi i possibili approcci per risolvere questo problema.
Cominciamo con un approccio intuitivo. Supponiamo di dover costruire un circuito che fosse chiuso quando tutti i n circuiti di relè di controllo funzionavano.
La soluzione a questo problema non richiede una lunga deliberazione: è chiaro che la condizione sarà soddisfatta se interconnessi in sequenza in contatti di relè normalmente aperti.
Allo stesso modo, è ovvio che per costruire un circuito che si chiude quando è intervenuto almeno uno dei n relè, è sufficiente collegare in parallelo n contatti di relè normalmente aperti.
È facile immaginare un circuito che si chiude quando vengono attivati alcuni relè, ma non tutti. Tale circuito è mostrato nella Figura 4, a. Sulla destra è un diagramma che opera secondo il principio di "tutto o niente". Verrà chiuso solo quando tutti i relè scattano o i relè sono scollegati (Figura 4, 6).
Considera ora un esempio più complesso. Supponiamo che ci siano n contatti situati in una determinata sequenza specifica: A, B, C, D, E, F ... Costruiamo un circuito che si chiude quando tutti i contatti collegati in serie k sono chiusi, e solo loro lo sono. Un tale schema per i valori n = 7 e k = 3 è mostrato nella Figura 4, c. Il metodo per costruire tali schemi per qualsiasi altro valore di n e k è chiaro da questa figura.
Procediamo alla costruzione di circuiti secondo le condizioni date del loro lavoro usando l'algebra di relè.
Come prima, le condizioni operative del circuito sono sempre sempre impostate verbalmente. Il progettista, prima di tutto, deve essere in grado di esprimere a parole ciò che vuole. Se non ha tale chiarezza, allora nessuna algebra aiuterà. Si dovrebbe sempre iniziare con una chiara dichiarazione dei requisiti impostati prima del nuovo schema. Come in ogni azienda, questo compito è forse il più difficile. Se le condizioni sono abbastanza semplici, allora possiamo immediatamente scrivere un'espressione di una formula strutturale che soddisfi questi requisiti.
Esempio 1 Supponiamo di dover costruire un circuito contenente 4 pin A, B, C e D in modo che il circuito sia acceso quando il contatto A è chiuso e uno degli altri tre contatti. In questo semplice caso, il funzionamento del circuito in forma di scrittura verbale sarà simile al seguente: “Il circuito dovrebbe condurre corrente se i contatti A e B sono chiusi, oppure i contatti A e C o i contatti A e D. D'accordo che ora è molto semplice elaborare una formula strutturale. Sarà simile a questo:
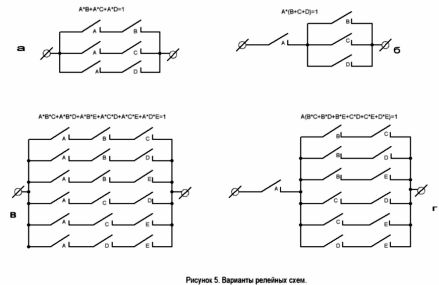
A * B + A * C + A * D = 1 o A * (B + C + D) = 1.
Il circuito ha due opzioni. Sono mostrati nella Figura 5. La seconda opzione non richiede un relè con tre contatti normalmente aperti.
Esempio 2 Il primo articolo era il compito numero 2 sul voto dei giudici sportivi. Leggi le sue condizioni più da vicino, è simile all'esempio appena esaminato. Una registrazione verbale più chiara dei requisiti sarà simile al seguente: “È necessario elaborare un circuito contenente 5 contatti A, B, C, D, E, in modo che conduca corrente e accenda la lampada del display se i seguenti contatti sono chiusi:
A e B e C, oppure A e B e D, oppure A e B ed E, oppure A e C e D, oppure A e C ed E, oppure A, D ed E. Il contatto A è il pulsante del presidente. Se non viene premuto, ciascuno dei 6 prodotti logici sarà 0, ad es. La votazione non ha avuto luogo.
La formula strutturale sarà la seguente:
(A * B * C) + (A * B * D) + (A * B * E) + (A * C * D) + (A * C * E) + (A * D * E) = 1,
oppure A * (B * C + B * D + B * E + C * D + C * E + D * E) = 1.
Entrambe le varianti del circuito sono mostrate nella Figura 5, C e D. Questa è la soluzione al problema.
Avendo una certa abilità nella lettura di formule strutturali, è facile immaginare il circuito dell'automa stesso e tutte le sue capacità. È interessante notare che l'algebra dei circuiti di relè fornisce più informazioni persino del circuito stesso. Ti permette di vedere quanti e quali relè sono richiesti. Con il suo aiuto, puoi facilmente trovare la versione più semplice della macchina a circuito.
Esempio 3 Avendo acquisito esperienza nella preparazione di formule strutturali, cercheremo di risolvere il problema iniziato primo articolo: devi progettare un interruttore che ti consenta di accendere la luce quando entri nell'ingresso e spegnerla dopo che sei salito al piano desiderato, o, al contrario, accenderla quando lasci l'appartamento e spegnerla dopo che sei scesa. La stessa situazione si verifica in un lungo corridoio: a un'estremità, la lampadina deve essere accesa e, dopo essere passata all'altra estremità, spenta. In breve, l'attività si riduce a controllare una lampadina da luoghi diversi con due interruttori.
Scegliamo la seguente procedura per risolvere il problema: in primo luogo, formuliamo chiaramente le condizioni operative degli interruttori, quindi le scriviamo sotto forma di una formula e disegneremo un circuito elettrico basato su di esse.
Quindi, che la lampadina ha bruciato (1), è necessario che sia soddisfatta una delle due condizioni:
1. Attivare l'interruttore in basso (A) e spegnere in alto (/ B). Entra nella veranda.
2. Attiva l'interruttore in alto (B) e spegni il fondo (/ A), quindi lascia l'appartamento.
Usando la notazione accettata, la formula strutturale è scritta come segue:
A * (/ B) + (/ A) * B = 1
Lo schema circuitale dell'interruttore è mostrato nella Figura 6. Attualmente, tali interruttori sono disponibili in commercio, questi sono i cosiddetti interruttori feedthrough. Pertanto, la considerazione di questi schemi qui è data semplicemente per il concetto dei principi generali del loro lavoro.
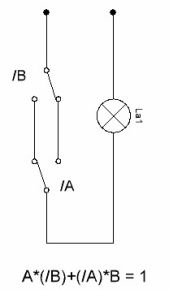
Figura 6
Nel task n. 1 all'inizio del primo articolo, stavamo parlando di uno schema che ti consente di accendere e spegnere la luce nella stanza con uno dei tre interruttori. Ragionando come nel caso di due interruttori, otteniamo la formula strutturale:
A * B * (/ C) + A * (/ B) + (/ A) * B * C = 1.
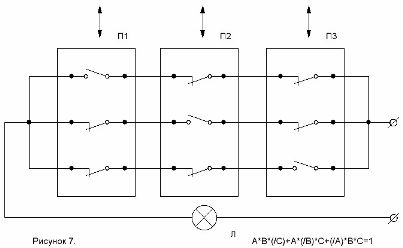
Lo schema elaborato da questa formula è mostrato nella Figura 7.
Figura 7
All'inizio del primo articolo, fu proposto un semplice compito educativo n. 2: come se nella stanza fossero presenti sei pareti e ognuna avesse un interruttore. La logica del circuito è esattamente la stessa dei tre interruttori. Indichiamoli con le lettere A, B, C, D, E, F. Ricordiamo che la notazione (/ A), (/ B) e così via, questo non è un segno di divisione, ma una negazione logica. Più spesso indicato da caratteri sottolineati e, anche da espressioni intere, in cima. In alcuni schemi, questo carattere di sottolineatura viene semplicemente sostituito da un segno meno. Quindi, la formula strutturale per i sei interruttori è:
(/ A) * B * C * D * E * F + A * (/ B) * C * D * E * F + A * B * (/ C) * D * E * F + A * B * C *
(/ D) * E * F + A * B * C * D * (/ E) * F + A * B * C * D * E * (/ F) = 1.
I lettori sono invitati a redigere un circuito elettrico completo che implementa questa formula strutturale per acquisire abilità pratiche nella progettazione di circuiti. Un piccolo suggerimento: per il circuito sono necessari sei relè, ognuno dei quali ha un contatto normalmente aperto e cinque normalmente chiusi. Relè così complessi, se necessario, possono essere assemblati da molti più semplici collegando le loro bobine in parallelo.
Questo conclude la storia dell'algebra booleana e dell'algebra dei circuiti dei relè.
Continuazione dell'articolo: Chip logici
Boris Aladyshkin
Vedi anche su electro-it.tomathouse.com
: