Algebra booleana. Parte 2. Leggi e funzioni di base

Continuazione della storia su algebra booleana, convenzioni, regole, operazioni. Transizione alle basi dei circuiti di contatto.

il primo articolo George Bull è stato descritto come il creatore dell'algebra della logica. Il secondo articolo descriverà le operazioni di base dell'algebra booleana e i metodi per semplificare le espressioni booleane. Quindi, l'algebra booleana usa le dichiarazioni come argomenti e non il loro significato, ma la verità o la falsità dell'affermazione.

Il modulo per scrivere espressioni nell'algebra booleana.

Se l'affermazione è vera, allora è scritta in questo modo: A = 1, se è falsa, quindi A = 0 (dopo tutto, non è vero che la patata è un frutto). Per ogni affermazione, A è vero (A = 1) o falso (A = 0). Non ci può essere un mezzo qui. Ne abbiamo già parlato.

Se si collegano due semplici istruzioni con l'unione E, si ottiene una dichiarazione complessa, che si chiama un prodotto logico. Prendiamo due semplici detti: "Tre è più di due" designeremo con la lettera A, "Tre meno di cinque" - con la lettera B.

Quindi il complesso detto "Tre è più di due e meno di cinque" è logico (in questo caso, la lettera maiuscola I indica che si tratta di un'operazione logica "AND", nonché più avanti nel testo "OR" e "NOT".) e B. È designato come segue: A ^ B o A * B.

Moltiplicazione logica (operazione "AND").

Nell'algebra elementare A * A = A2. Ma nell'algebra di Buhl A * A = A2 = A, A * A = A, poiché il segno di moltiplicazione (*) ora significa ... E ... nel senso di E ... E. Tutta la nostra esperienza conferma che l'A & A è uguale al solo A. Non si può essere in disaccordo con questo. La verità dell'affermazione non cambia se viene ripetuta dal fattore più volte.

Il prodotto di due affermazioni è considerato vero (uguale a 1), quindi, e solo se entrambi i fattori sono veri, e falso (uguale a 0) se almeno uno dei fattori è falso. Concordo sul fatto che queste regole non contraddicono il buon senso e, inoltre, sono pienamente conformi alle regole dell'algebra elementare:

1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.

La prima uguaglianza recita come segue: se sia A che B sono veri, allora il prodotto A * B è vero. Nell'algebra di Buhl, il segno di moltiplicazione (*) sostituisce l'unione I.

I prodotti logici possono includere non due, ma un numero maggiore di dichiarazioni - fattori. E in questo caso, il prodotto è vero solo quando allo stesso tempo tutti i fattori-dichiarazioni sono veri.

Aggiunta logica (operazione OR)

Se due dichiarazioni sono collegate da un sindacato OR. quella frase composta formata si chiama somma logica.

Considera un esempio di una somma logica. Dicendo A: "Oggi andrò al cinema".

Dichiarazione B: "Oggi andrò in discoteca". Aggiungiamo entrambe le dichiarazioni e otteniamo: "Oggi andrò al cinema O in discoteca".

Questa affermazione complessa è indicata come segue: A + B = C o (A V B) = C.

Con C abbiamo indicato un'affermazione complessa di una somma logica.

Nell'esempio in esame, l'unione OR non può essere utilizzata in senso esclusivo. In effetti, lo stesso giorno puoi andare al cinema e in discoteca. Ed ecco il detto:

"Il presidente dell'associazione di giardinaggio sarà Petrov o Ivanov", non è una somma logica, perché solo una persona sarà il presidente e l'altra sarà un giardiniere ordinario dilettante.

Il segno V per la somma logica è scelto perché è la lettera iniziale della parola latina "vel", che significa "o", in contrasto con la parola latina "aut>, che significa" e ". Ora dovrebbe essere chiaro a tutti perché il prodotto logico è indicato dal segno ^.

Nell'algebra elementare esiste una regola A + A = 2A. Questa regola è vera, indipendentemente dal numero rappresentato dalla lettera A. Nell'algebra booleana, la regola A + A = A corrisponde ad essa. Tutta la nostra esperienza di vita dice che dire A OR A o entrambi A è solo un altro modo più lungo per dire solo A.

Come ogni istruzione composta, la somma delle due istruzioni A e B può essere vera o falsa. La somma è considerata vera, cioè uguale all'unità, se almeno uno dei termini è vero:

A + B = 1 se OR A = 1 OR B = 1, che è coerente con l'aritmetica convenzionale:

1+0 = 0+1 = 1.

Se entrambe le affermazioni sommate sono vere, allora anche la somma è considerata vera, quindi, nell'algebra booleana abbiamo: (1) + (1) = 1.

Le parentesi sono impostate qui per enfatizzare il condizionale, il significato di questa aggiunta e non l'aritmetica.

La somma di due affermazioni è considerata falsa e uguale a zero se, ma solo se entrambi i termini sono falsi. Da qui:

0 + 0=0.

Quindi, la somma delle due affermazioni A + B è considerata vera se vera, OR A, OR B, OR entrambi i termini insieme. Pertanto, la parola OR è indicata dal segno +.

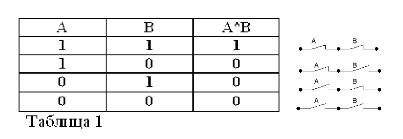
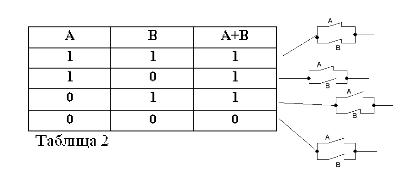
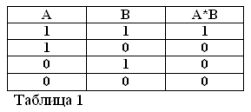
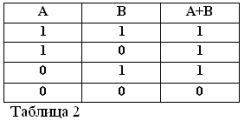
Ricordando che le affermazioni A e B possono essere solo vere o false e, quindi, avere una misura della verità 1 o 0, i risultati delle operazioni AND e OR considerate possono essere riassunti nelle tabelle 1 e 2.

La terza operazione, ampiamente utilizzata dall'algebra di Buhl, è l'operazione di negazione - NON. Ti ricordiamo che l'algebra elementare usa le operazioni ADD, D Subtract, Moltiplica per, Divide per e alcune altre.

Per ogni affermazione A, c'è la sua negazione NON A, che indicheremo con il simbolo / A. Questo non dovrebbe essere in dubbio.

Diamo esempi: "Andremo nella foresta" A, "Non andremo nella foresta" / A.

Se l'affermazione A è vera, cioè A = 1, allora la sua negazione / A deve essere falsa / A = 0. E viceversa, se un'affermazione è falsa, allora la sua negazione è vera. Ad esempio: "Un cavallo non mangia fieno" / A = 0, "Un cavallo non mangia fieno" (A = 1). Questo può essere espresso nella tabella 3.

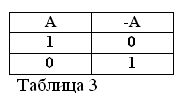
Determinando il significato dell'azione della negazione e assumendo che delle due affermazioni A e / A sia sempre una vera, seguono due nuove formule dell'algebra booleana:

A + (/ A) = 1 e A * (/ A) = 0.

Esistono anche altre formule che semplificano l'elaborazione logica delle istruzioni. Ad esempio, 1 + A = 1, poiché, secondo la definizione di addizione, nel caso in cui un termine sia uguale all'unità, la somma è sempre uguale all'unità. Il risultato ottenuto non dipende dal fatto che A = 0 o A = 1.

Ognuna delle tre operazioni logiche che abbiamo esaminato (AND, OR, NOT) ha determinate proprietà che sono vicine alle regole dell'algebra elementare. Se tutti sono formulati, allora otteniamo 25 regole di algebra booleana. Sono abbastanza per risolvere quasi ogni problema logico. Senza queste regole, diventa abbastanza difficile risolvere i problemi logici a causa della loro apparente complessità. Cercare di trovare la risposta corretta senza usare le regole significa sostituirle con ingegnosità e ragionamento generale. Le regole facilitano notevolmente questo lavoro e fanno risparmiare tempo.

Nel quadro dell'articolo, è impossibile considerare tutte queste 25 regole, ma chi lo desidera può sempre trovarle nella letteratura pertinente.

Come già accennato nel primo articolo del 1938, il giovane scienziato americano Claude Shannon nel suo articolo "Analisi simbolica dei circuiti di commutazione e di commutazione" utilizza per la prima volta l'algebra booleana per problemi di tecnologia dei relè. La scoperta di Shannon fu che si rese conto che il metodo di progettazione di macchine a relè e computer elettronici è in realtà un ramo della logica matematica.

Succede spesso Per molti anni, lo scienziato ha lavorato su un problema che sembra del tutto inutile per i suoi connazionali - semplicemente divertente. Ma passano decenni e talvolta secoli e una teoria di cui nessuno ha bisogno non solo acquisisce il diritto di esistere, ma senza di essa ulteriori progressi diventano impensabili.

Cosa ha aiutato Shannon la seconda volta a "scoprire" l'algebra booleana? Il caso? Niente del genere.

L'amore per le macchine a relè, basate su interruttori e relè convenzionali, ha aiutato il giovane scienziato a collegare una teoria dimenticata con i compiti degli scambi telefonici automatici, sui quali ha lavorato in quel momento. Successivamente, Shannon introdusse la stessa idea di "sì o no" nei messaggi discreti e gettò le basi per un'intera sezione della cibernetica: la teoria dell'informazione.

L'algebra di Buhl era molto adatta per l'analisi e la sintesi di circuiti a relè. È stato sufficiente accettare come una vera affermazione: "C'è un segnale nel circuito", e come falso - "Non c'è segnale nel circuito", come è apparsa una nuova algebra - l'algebra del segnale, l'algebra del circuito del relè.

La nuova algebra è valida solo per la considerazione di relè e circuiti di commutazione. Dopo tutto, solo in tali schemi è soddisfatta la condizione "c'è un segnale" e "nessun segnale". Laddove il segnale cambia continuamente, acquisendo un numero arbitrariamente elevato di condizioni intermedie (tale segnale è chiamato analogico), l'algebra del relè non è applicabile. Questo deve essere sempre ricordato. Ma solo la maggior parte dei computer elettronici e delle macchine cibernetiche utilizza il principio discreto dell'elaborazione del segnale, che si basa sugli elementi "sì - no".

L'espressione "Contatto chiuso" è stata accettata da Shannon come vero (1) e "Contatto aperto" come falso (0). Il resto dell '"algebra", comprese le operazioni AND, OR, NOT e 25 regole, Shannon prese in prestito da Boole.

L'algebra del circuito di relè si è rivelata più semplice dell'algebra booleana, poiché tratta solo elementi del tipo "sì - no". Inoltre, la nuova algebra è più visiva.

Gli elementi di questa algebra sono i contatti, che indicheremo con le lettere A, B, C ... Il contatto è chiuso - A, il contatto è aperto - / A (lettera con un trattino).

La notazione, come vedi, è completamente presa dall'algebra booleana. Un contatto aperto è una negazione di un contatto chiuso. Lo stesso contatto non può essere sia chiuso che aperto.

Siamo d'accordo che se in qualsiasi circuito due contatti sono indicati dalla stessa lettera, ciò significa che assumono sempre gli stessi valori.

In un dato momento, entrambi sono aperti contemporaneamente o entrambi sono chiusi. Il modo più semplice di immaginarli collegati meccanicamente in modo che entrambi si aprano o si chiudano contemporaneamente.

Se in una catena un contatto è una negazione di un altro contatto, allora i loro significati sono sempre opposti. Ad esempio, i contatti C e / C non possono mai essere contemporaneamente aperti o contemporaneamente chiusi. E nel diagramma possono essere rappresentati meccanicamente connessi: se uno di essi si apre, l'altro si chiude.

Iniziamo la nostra conoscenza dell'algebra dei relè analizzando i circuiti più semplici corrispondenti alle operazioni AND, OR e NOT.

Il prodotto di due contatti (operazione AND) è il circuito ottenuto come risultato della loro connessione in serie: è chiuso (uguale a 1) solo quando entrambi i contatti sono chiusi (uguale a 1).

La somma di due contatti (operazione OR) sarà il circuito formato quando sono collegati in parallelo: è chiuso (uguale a 1) quando almeno uno dei contatti che formano il circuito è chiuso (uguale a 1).

Il contrario di questo contatto (operazione NON) è un contatto uguale a 0 (aperto) se questo contatto è 1 (chiuso) e viceversa.

Come nell'algebra booleana, se i contatti sono indicati dalle lettere A e B, indicheremo il prodotto di due contatti con A * B, la somma di A + B e il contatto opposto A, con / A. Quanto sopra è spiegato nelle figure 1, 2 e 3.

Validità delle tabelle corrispondenti alle operazioni AND, OR e NOT. ora nessuno dovrebbe essere in dubbio.

Soffermiamoci su due esempi: 1 * 0 = 0 e 1 + 0 = 1.

Si può vedere dalla figura che un contatto permanentemente chiuso collegato in serie con un contatto costantemente aperto equivale a un contatto permanentemente aperto (1 * 0 = 0) Un contatto permanentemente chiuso collegato in parallelo con un contatto costantemente aperto equivale a un contatto permanentemente chiuso.

Avendo familiarità con l'aritmetica dei circuiti di contatto, è possibile descrivere qualsiasi circuito di relè con una formula utilizzando le convenzioni accettate. Nella cibernetica, tali formule sono chiamate strutturali.

Se la formula strutturale di qualsiasi circuito di relè è 1, allora un segnale può passare attraverso di esso - il circuito è chiuso. Al contrario, se la formula strutturale del circuito è 0, il segnale non passerà attraverso di esso - il circuito è rotto.Conclusione: due circuiti di relè sono equivalenti tra loro quando le loro formule strutturali sono uguali.

Nel seguito dell'articolo, prenderemo in considerazione esempi di circuiti di contatto, circuiti di contatto tipici e loro equivalenti, nonché l'elaborazione di diagrammi secondo le formule strutturali. Consideriamo anche i principali circuiti logici che svolgono le funzioni dell'algebra booleana.

Continuazione dell'articolo: Algebra booleana. Parte 3. Schemi di contatto

Boris Aladyshkin

Comments

[#1 alex]

Grazie

Un solo punto, paragrafo:

"Come nell'algebra booleana, se i contatti sono indicati dalle lettere A e B, indicheremo il prodotto di due contatti con A * B, la somma di A + B e il contatto opposto A, con / A. Quanto sopra è spiegato nelle figure 1, 2 e 3 ..."

Dov'è la figura 3?